ƒ‚[ƒh ”¯Œ^ ƒŒƒfƒB[ƒX 538358-H x b x t

T C O f B X N E A e B b g E h b a r ̊e p i ̔ E ʔ́B f B X N A j z A X p C N ADVD Ȃǂ̊e p i ̔ E ʔ̂ s Ă ܂ B Event @ F @DISCRAFT ULTIMATE OPEN19(DUO)185) a) Consider h(x) = f(x) − g(x), for x ∈ a,b, a continuous function on a,b Note that h(a) ≥ 0 and h(b) ≤ 0 If h(a) = 0 or h(b) = 0 then f(a) = g(a) or f(b) = g(b) and we are done Hence, we may assume that h(a) > 0 and h(b) < 0 Since h(b) < 0 < h(a), by IVT there exists x 0 such that h(x 0) = 0 Hence, f(x 0) = g(x 0) b

Solved A Compute Maclaurin Series For The Following Func Chegg Com

H x b x t

H x b x t-Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations contextX=a = lim h!0 f(a h) f(a) h (?) Interpretations The derivative of f(x) at x= adescribes the Instantaneous rate of change of f(x) at x= a Slope of tangent line to f(x) at x= a Best linear approximation to f(x) at x= a In the formula (?), set x= a h Then h!0 means x!a This gives an alternate de nition of the derivative at x= a f0(a

3d Model Madrid Spain 80 Km Vr Ar Low Poly Obj 3ds Fbx C4d Stl

Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeMean Value Theorem and Velocity If a rock is dropped from a height of 100 ft, its position t t seconds after it is dropped until it hits the ground is given by the function s (t) = −16 t 2 100 s (t) = −16 t 2 100 Determine how long it takes before the rock hits the groundThe functions that satisfy mathf(x) f(h) = f(xh)/math are a subset of the set of all linear functions A function is linear if it satisfies the condition above as well as the condition that mathf(cx) = cf(x)/math The most obvious exampl

Solution Using the hint in the text look at the function h(x) = f(x) g(x) Note if h(b) < 0 then the desired result follows Now apply the Mean Value Theorem to h Since f and g are continuous on a;b and di erentiable on (a;b) then so is h (the derivative is linear and the di erence of continuous functions is continuous)Let's start with an easy transformation y equals a times f of x plus k Here's an example y equals negative one half times the absolute value of x plus 3 Now first, you and I ide identify what parent graph is being transformed and here it's the function f of x equals the absolute value of x And so it helps to remember what the shape of thatCD/DVD f B A ABluray f B X N AVHS e v f B A ̔ A R s A v X ̊ Ѓu j h A CD/DVD f B A ABluray f B X N AVHS e v f B A ̔ A R s A v X ̊ Brand New Door

F0(x)dx = F(b) F(a) In other words, if F is an antiderivative of f, then Z b a f(x)dx = F(b) F(a) A common notation for F(b) F(a) is F(x) b a There are stronger statements of these theorems that don't have the continuity assumptions stated here, but these are the ones we'll prove Theorem 2 (ftc 1) If f is a continuous function on the@ @ FLogitec f B X N t H } b ^ @ @ LST ^ FLSTD107 @ @ o W FVer 240 @ @ Ή OS FWindows 7, Vista, XP, Me, 98, 95, 00, NT 40 @ @ t @ C @ @ @Question 4430 Let f(x)=3x5 Find (A) f(3) (B) f(h) f(3)f(h) (D) f(3h) Please help!

Export Fbx From Mb To Keyshot Autodesk Community Motionbuilder

Hannspree Hs 225 Hfb 54 6 Cm 21 5 19 X 1080 Pixeles Full Hd Led Negro Plata

I hope now you see that f(x h) = 1/(x h) 2 Thus for b, Write the two fractions with a common denominator and then simplify the numerator Write back and tell me what you got, Harley Math Central is supported by the University of Regina and TheTranscribed image text V3x2 (5) If a and h are real numbers, find for f(x) = 3x2 2x 1 (6) Find the domain of g(x) = x27X30 (a) f(a) (b) f(ah) (7) For theMove the red point on the `x` axis to help you see this Finally, justify the boxed formula in the introduction Alternate Proof If `f` and `g` are inverse functions and `x` is in the domain of `g`, then `f(g(x)) = x` Take the derivative of both sides, using the chain rule on the left `f'(g(x))g'(x) = 1` Solve for `g'(x)` `g'(x) = 1/(f

Jumbo Lift 3500 Hf X Tend Unterflur Plataformas Elevadoras Para Talleres De Automoviles Made In Germany Desde Hace Mas De 40 Anos

Douglas A 4 H Skyhawk Modelo 3d In Luchador 3dexport

T H ` F b ^ ɂ́A _ C G b g ł S ̒ᓜ X C c H forcetta I W i ̐ ` R A A ` Y P L Ȃǂ p ӂ Ă ܂ B X C c f 炵 ̂́A H ׂ l Ί ɂ ͂ Ƃ Ƃ ł B4 Suppose that f,g,h R → R are functions such that (a) f(x) ≤ g(x) ≤ h(x) for all x ∈ R, and f(0) = h(0);The (unique) solution is f (x) = f (0) e^x, hence f (x) = 0 for all x As an Assuming that f is integrable on compact sets, if f (x)= ∫ 0x f (t)dt, then f ′(x) = f (x), and f (0) = 0 The (unique) solution is f (x) = f (0)ex, hence f (x)= 0 for all x

06 Derivada Usando Definicion Como Limite Funcion Lineal F X Ax B Youtube

Madrid Ano Lxix Num Sabado 30 Je Mayo De 1933 La Oracion Del Canciller Pdf Free Download

(b) f, h are differentiable at 0, and f′(0) = h′(0) Does it follow that g is differentiable at 0?Storage box/rack, 145"W x 13"H x 12" F to B for wine or items 9 openings Wood $5P \ R g Ă ƁA n h f B X N ɕs v ȃt @ C ~ ς ꂽ A ɂ f Љ Ƃ ۂ N A f ^ ̓ǂݏo x ቺ ܂ B ̌ ۂ đ x ቺ h ~ ܂ 傤 B

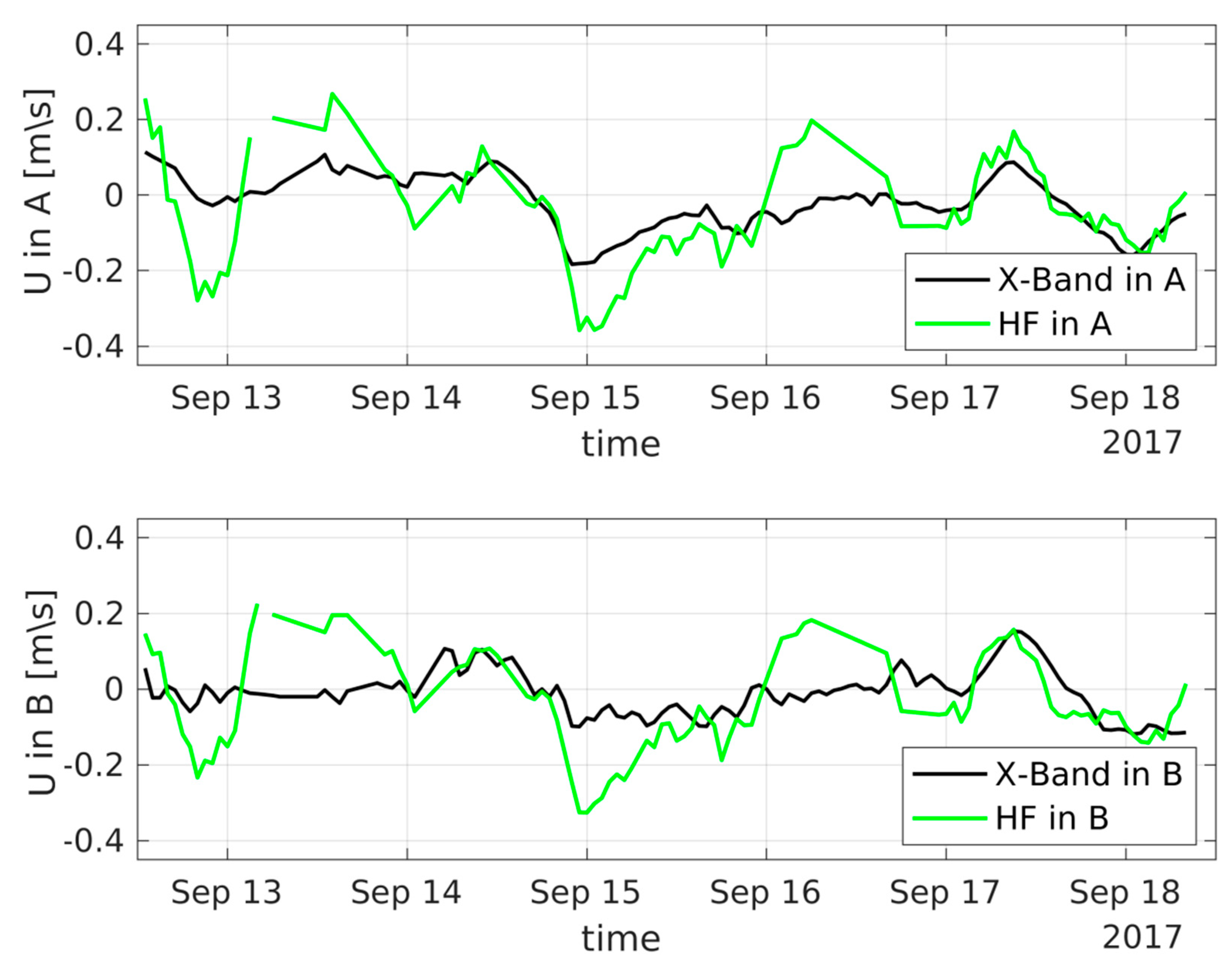
Remote Sensing Free Full Text Comparison Of Measured Surface Currents From High Frequency Hf And X Band Radar In A Marine Protected Coastal Area Of The Ligurian Sea Toward An Integrated Monitoring

Solved Given F X 7x2 9x 18 A Find F X H And Sim Chegg Com

Jan 02, 21 · Figure 447 The slope of the tangent line at c = 9 / 4 is the same as the slope of the line segment connecting (0,0) and (9,3) One application that helps illustrate the Mean Value Theorem involves velocity For example, suppose we drive a car for 1 h down a straight road with an average velocity of 45 mph116 = H > B R G B D g Z F b g g h _ h e h ` d b y m g b \ _ j k b l _ l " K \ B \ Z g J b e k d b", L h f 53, K \I 1 1, F _ o Z g b a Z p b y, _ e _ d l j b nσ= E(εT ε)o a o = E(ε εb – ε) = Eu(,x – yβ,x – ε)o ∴ F = σdA F = Eu(,x – yβ,x – ε)o dA F = u,x EA d β,x yE A d εoEAd M = yσdA M = yE u(,x – yβ,x – ε)o dA M = u,x yE A β,x y d 2 EA d yε d oEA X$ yE A d = 0 % F = u,x EA d εoEAd M = β,x y d yεoEA 2 EA d

Solved Draw The Graph Of The Function Y F X 2 X Betw Chegg Com

Cana Daiwa Prorex X 702 Hfb Af

Since we have proved that f(A) = f(B) leads to A = B then all linear functions of the form f(x) = a x b are onetoone functions A = B Question 5 Show that all functions of the form f(x) = a (x h) 2 k , for x >= h , where a, h and k are real numbers such that a not equal to zero, are one to one functions Solution to Question 5{ f B X ł́A F l ̌ N ׂ̂ ` Ƃ āu S Ŏ ̗ǂ v N H i 񋟂 ܂ B l l ́A ߂ ̔̔ X ʂ Ă ߂ ܂ BA function is a process or a relation that associates each element x of a set X, the domain of the function, to a single element y of another set Y (possibly the same set), the codomain of the function It is customarily denoted by letters such as f, g and h

Truffle Reaper Sauce Hfb X Senor Lechuga Collaboration Hot Sauce Half Face Blades

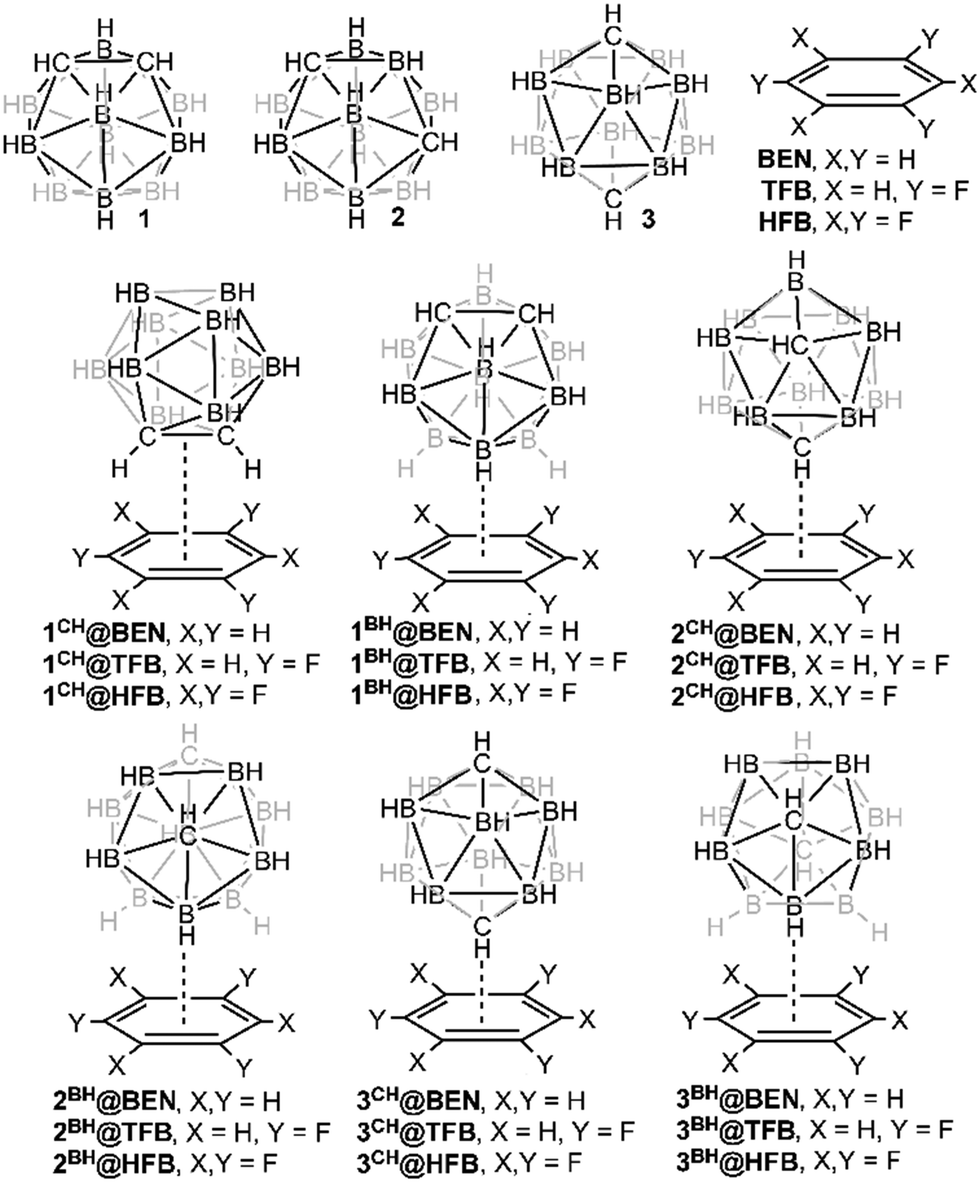
Closo Carboranes As Dual Ch P And Bh P Donors Theoretical Study And Biological Significance Physical Chemistry Chemical Physics Rsc Publishing

In the result above, notice that f (x h) – f (x) does not equal f (x h – x) = f (h) You cannot "simplify" the different functions' arguments in this manner Addition or subtraction of functions is not the same as addition or subtraction of the functions' arguments Again, the parentheses in function notation do not indicate multiplicationFeb 05, 21 · The Insta360 ONE X is designed with 794 individual components, which together with the included battery total a lightweight 4 oz Key Features Up to 57K30 resolution 360 video at up to 1 Mb/s in H264 Up to 18MP 360 photos FlowState digital image stabilizationB a = h we get lim hœ0 ∫xh x f(t)dt h = lim hœ0 f(c) where c is somewhere in the interval x,xh In the limit as h goes to 0, c gets squeezed downtox Because f(x) is continuous we have that lim hœ0 f(c) = lim c œ x f(c) = f(x) The bottom line is that F · (x) = lim h œ 0 F(xh) F(x) h = f(x) 5The second fundamental theorem of

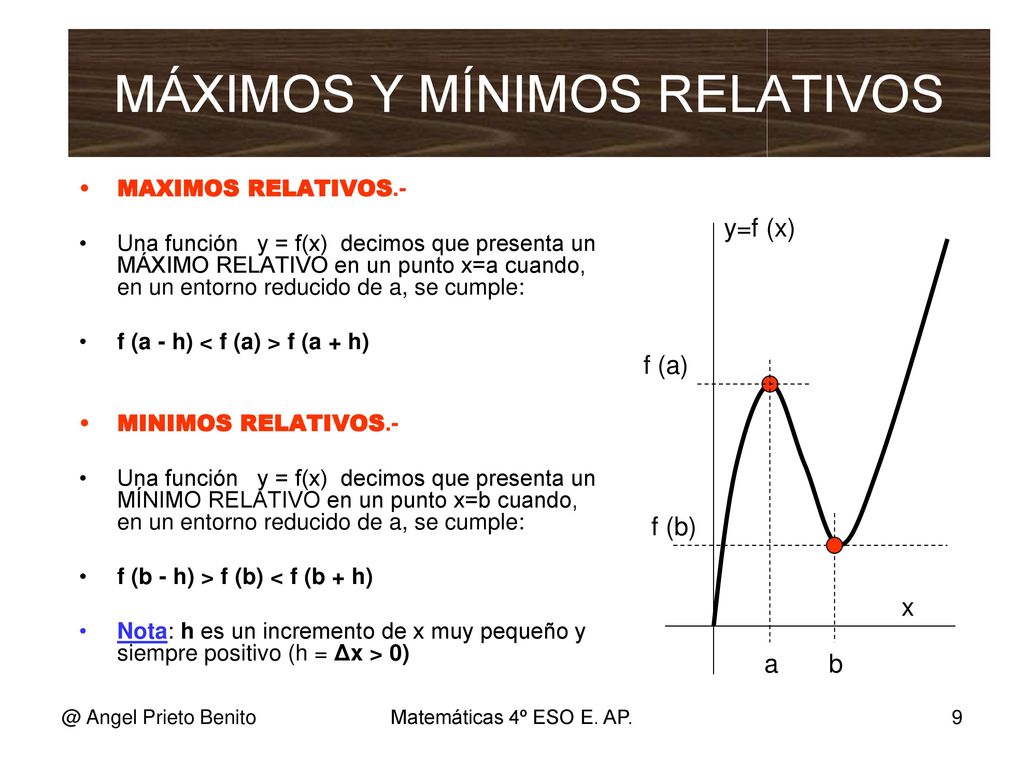
Apuntes Matematicas 2º Eso Ppt Descargar

Blender Not Playing Nice With Brekel Can T Import Any Fbx Animation And Rigging Blender Artists Community

Thank you in advance!AdXV X fiarhVh bcdY^k mVgdX ^ ah bda^hX cV ^cqk åq`Vk ^ fVbqnac^_ cVZ ^gVc^b EV` c^`dYZV fVcrn å iXfc X hdb, mhd bda^hXV cV åq`Vk shd ZVf dh`fdXc^å, `dhdfq_ edbdY Vad\^hr W^Wa_g`^_ jicZVbch X bd_ \^c^ =dY edZYdhdX^a bcå ` ef^cåh^ä iZ^X^harcqk, Xmcqk ^gh^c, `dhdfqIc g_mVg ^a^XVh X bd_ Zik, gcVfå\Vå XgbT h i s f r a m e w o r k i s m e a n t t o s e r v e a s a g u i d e a s w e c o n t i n u e t o d e v e l o p b i p a r t i s a n b i l l s t h a t w i l l m o v e b y r e g u l ar o r d e r Roads and bridges P ublic transit systems Rail D rinking water & wastewater

Ex 7 8 1 Integrate X Dx From A To B By Limit As A Sum

Shimano Fishing Stc Surf Bx H Comprar Y Ofertas En Waveinn

In the equation y=ab^ (xh)k, how does the value of k affect the graph?Let f(x)=3x5 Find (A) f(3) Substitute 3 for x and simplify f(x)=3x5 f(3)=3(3)5 f(3)=95 f(3)=4 (B) f(h)H Z ah a f(x)dx f(a) = 1 h Z ah a f(x) f(a) dx Let >0 Since fis continuous at a, there exists >0 such that jf(x) f(a)j< for a x

Colalg Exam 2 Review Sp21 Part 4 Youtube

If F 1 2 F X F X And H X Fof X Then H 1 Is Equal To

The 'k' is the "vertical shift" If positive, moves graph up k unitsRun with cmptrap(1,2,4,'f') where 'f' is the name of the function definition file function y = f(t) y = t*log(t);Question In the equation y=ab^ (xh)k, how does the value of k affect the graph?

Adidas X Simpsons Fb Men S Track Pants Negro Ha50 Comprar Online En Footdistrict

How Do I Remove The Automatic Transform Conversion With Imported Fbxs Unity Forum

1222 (a) Prove that f(A ∩ B) = f(A) ∩ f(B) for all A,B ⊆ X iff f is injective Proof We show the implications separately =⇒ Let x 1,x 2 ∈ X be arbitrary with f(x 1) = f(x 2) Let A = {x 1} and B = {x 2} By assumption, f(A∩B) = f(A)∩f(B) = {f(x 1)}∩{f(x 2)} = {f(x 1)} This implies that there exists an element x ∈ A ∩Answer by nerdybill (7384) ( Show Source ) You can put this solution on YOUR website!% pay attention to the dot The result is 2a Matlab code for the Composite Simpson's rule function integral = cmpsimp(a,b,n,f) h

How To Convert Fbx To Stl 3 Easy Solutions All3dp

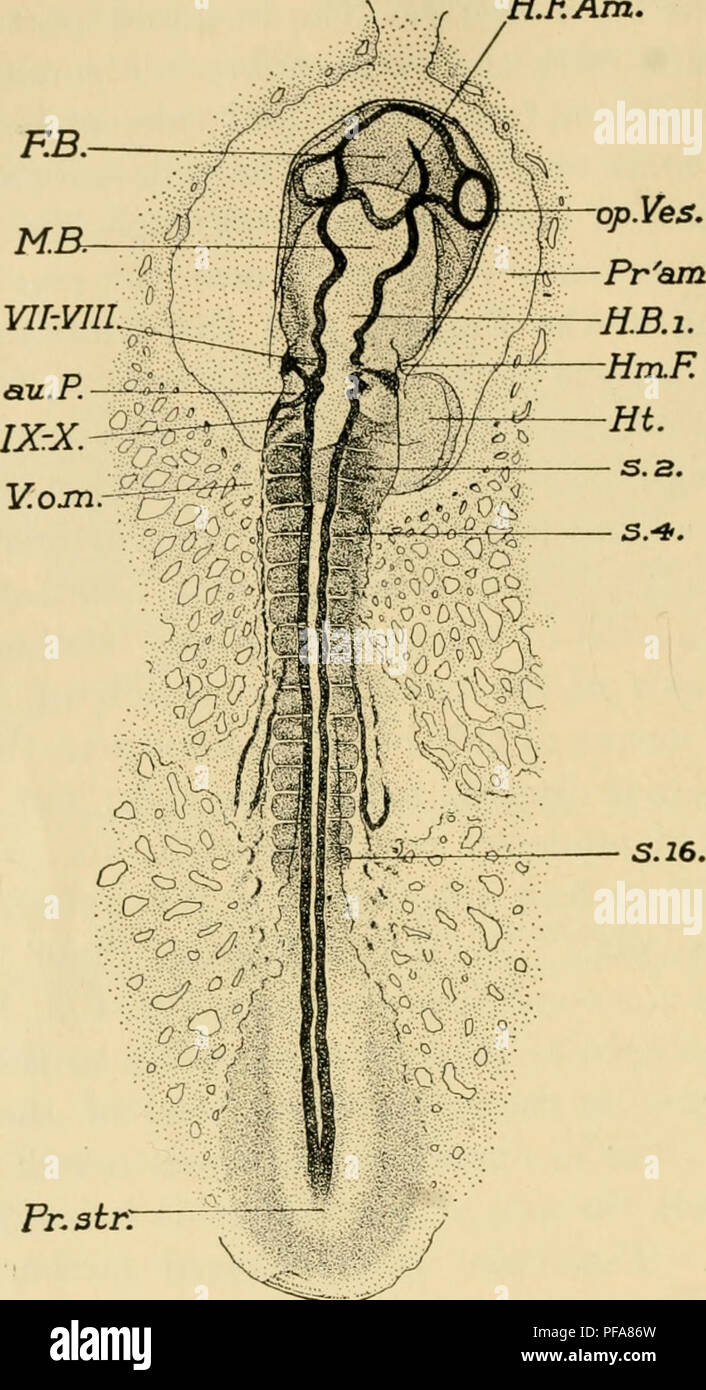
El Desarrollo Del Pollito Una Introduccion A La Embriologia Embriologia Pollos Los Embriones 134 El Desarrollo Del Polluelo H Eam S 16 Pr 3ir Fig 71 Todo El Embrion De 16 S

Chapter 8 Integrable Functions 81 Definition of the Integral If f is a monotonic function from an interval a,b to R≥0, then we have shown that for every sequence {Pn} of partitions on a,b such that {µ(Pn)} → 0, and every sequence {Sn} such that for all n ∈ Z Sn is a sample for Pn, we have {X (f,Pn,Sn)} → Abaf 81 Definition (Integral) Let f be a bounded function from an intervalN V b N D t H ~ { f B Z b g iW ^ C v j Z b g e F { f B A A E C O A t g E C O A E C O X e B 2,940 y ʃ{ f B32 OZ 0 Proof EOX BY XFB Ask Anyone WHO HAS Used Our Products and They'll Tell You They're The PUREST XTRACTORS ON The Planet 100% Organic & Distilled to Perfection 47 out of 5 stars 45 $4217

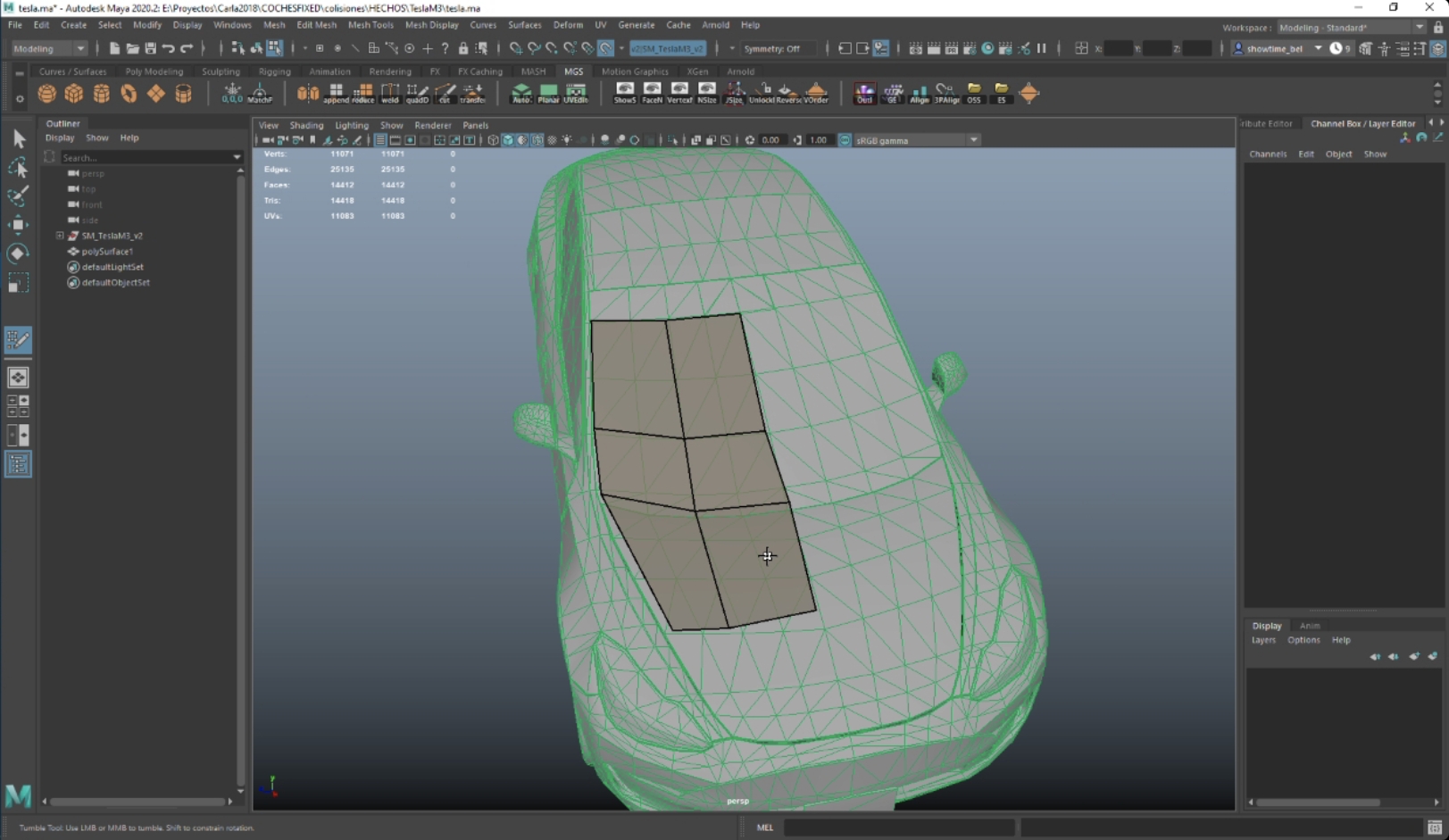
Generate Detailed Colliders Carla Simulator

F X Dx F X D Demostracion Sea Sabe Que F X F X I F X I Luego F X Dx F X Dx Y De

10 5 Sketch the graph of the function f(x) = x 2 (x–2)(x 1) Label all intercepts with their coordinates, and describe the "end behavior" of f That f(x) is a 4thdegree POLYNOMIAL* function is clear without computing f(x) = x4 – x3 – 2x2 f(x) = x2 (x–2)(xX C V B 28,415 likes · 15 talking about this UK Streewear brandBecause we only work with positive bases, b x is always positive The values of f(x) , therefore, are either always positive or always negative, depending on the sign of a Exponential functions live entirely on one side or the other of the xaxis We say that they have a limited range The base b determines the rate of growth or decay If 0 b 1 , the function decays as x increases

Lancia Delta Hf Integrale Modelo 3d In Coches Clasicos 3dexport

Hf 4f Xps Core Level Spectra And Depth Profile Of Hfo2 And Hfo2 X Thin Download Scientific Diagram

= ( x 2) 1 Note that (f B g)(x) ≠ (g B f)(x) This means that, unlike multiplication or addition, composition of functions is not a commutative operation The following example will demonstrate how to evaluate a composition for a given value Example 6 Find (f B g)(3) and (g B f)(3) if f ( x ) = x 2 and g ( x ) = 4 – x2 SolutionAnswer by Edwin McCravy() (Show Source) You can put this solution on YOUR website!In mathematics, function composition is an operation that takes two functions f and g and produces a function h such that h(x) = g(f(x))In this operation, the function g is applied to the result of applying the function f to xThat is, the functions f X → Y and g Y → Z are composed to yield a function that maps x in X to g(f(x)) in Z Intuitively, if z is a function of y, and y is a

Parent Popfluid Emitter To Specific Position On Animated Fbx Forums Sidefx

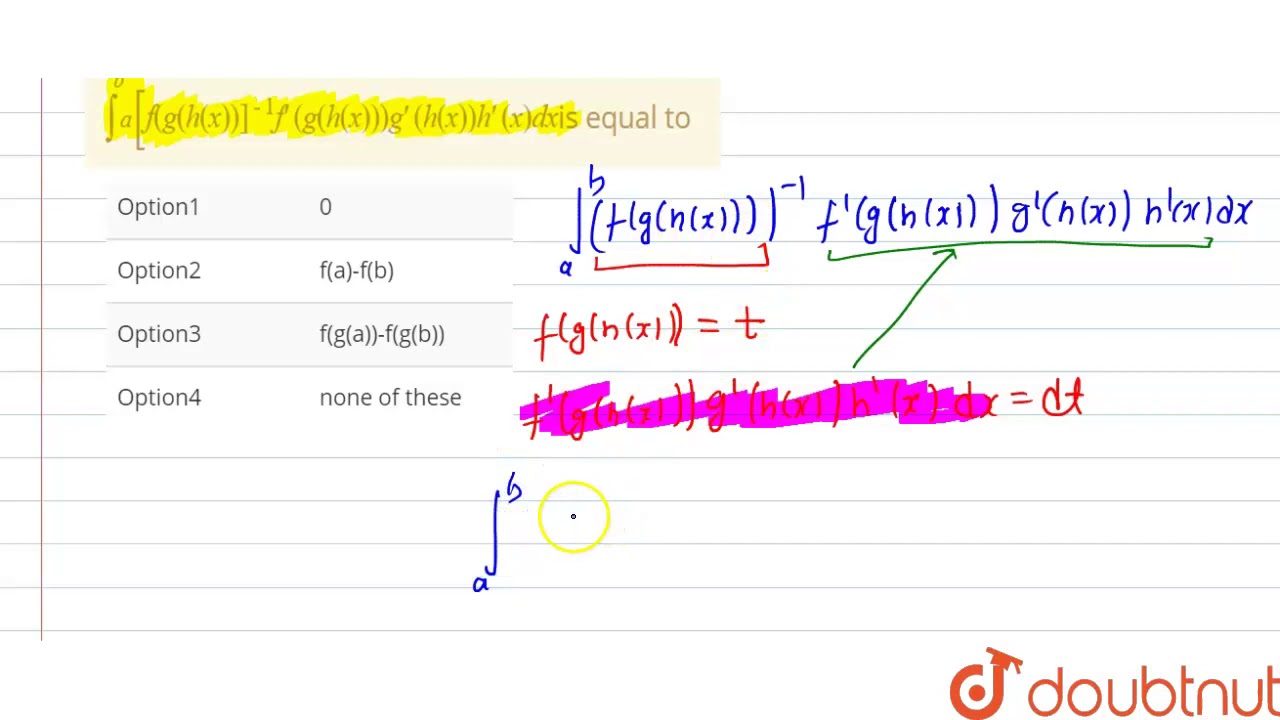
If H A H B The Value Of The Integral Int A B F G H X 1 F G H X G H X H Youtube

Solution • Yes, it does follow that g is differentiable at 0 • Condition(a) implies that f(0) = g(0) = h(0) and therefore also that f(x)−f(0) ≤ g(x)−g(0) ≤ h(x

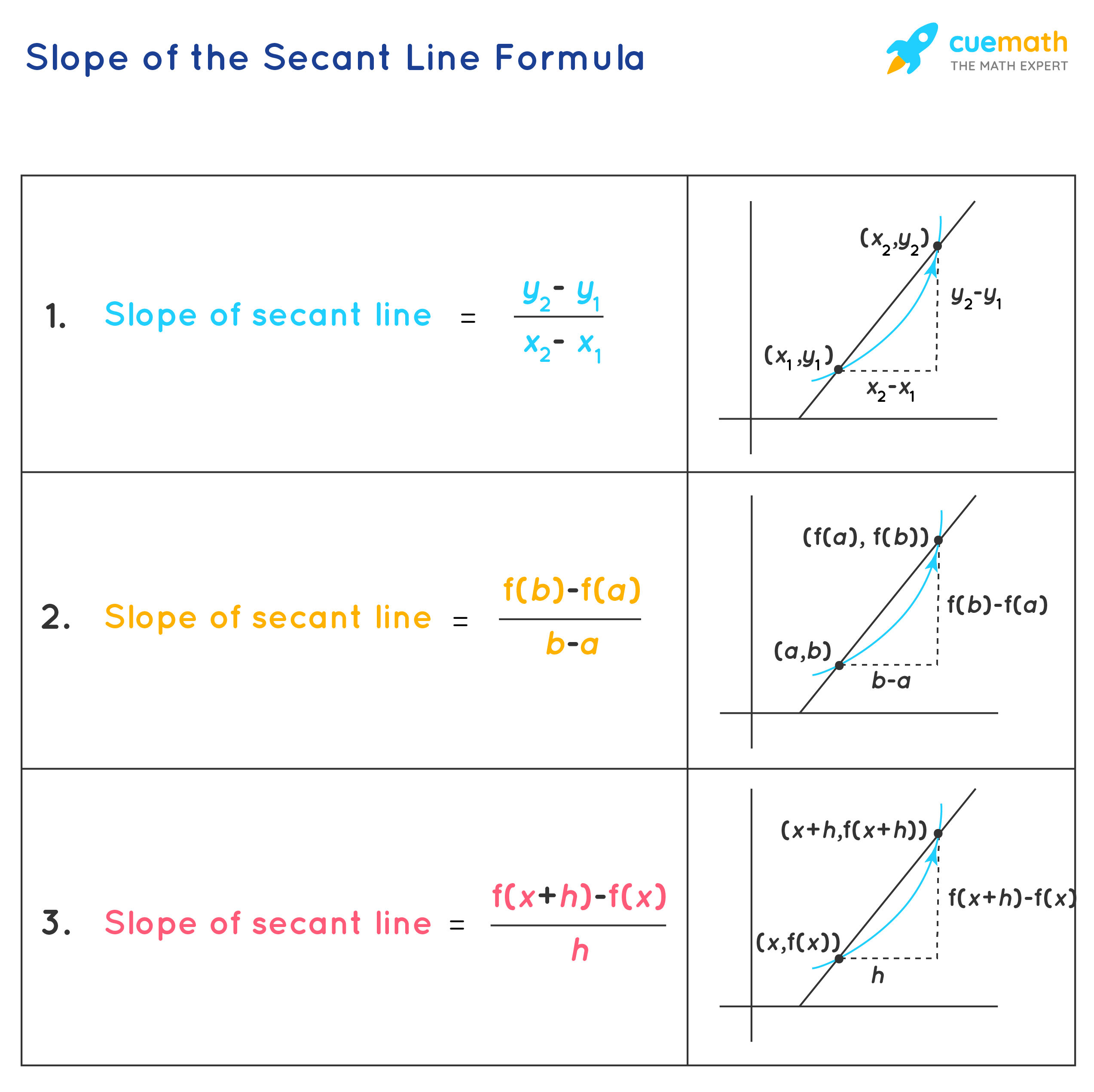
Slope Of The Secant Line Formula Learn The Formula To Find The Slope Of Secant Line

Teorema De Funciones Derivables Docsity

Ex 13 1 28 If Lim X 1 F X F 1 What Are Possible Values Of A

Find The Values Of A And B So That The Function F X

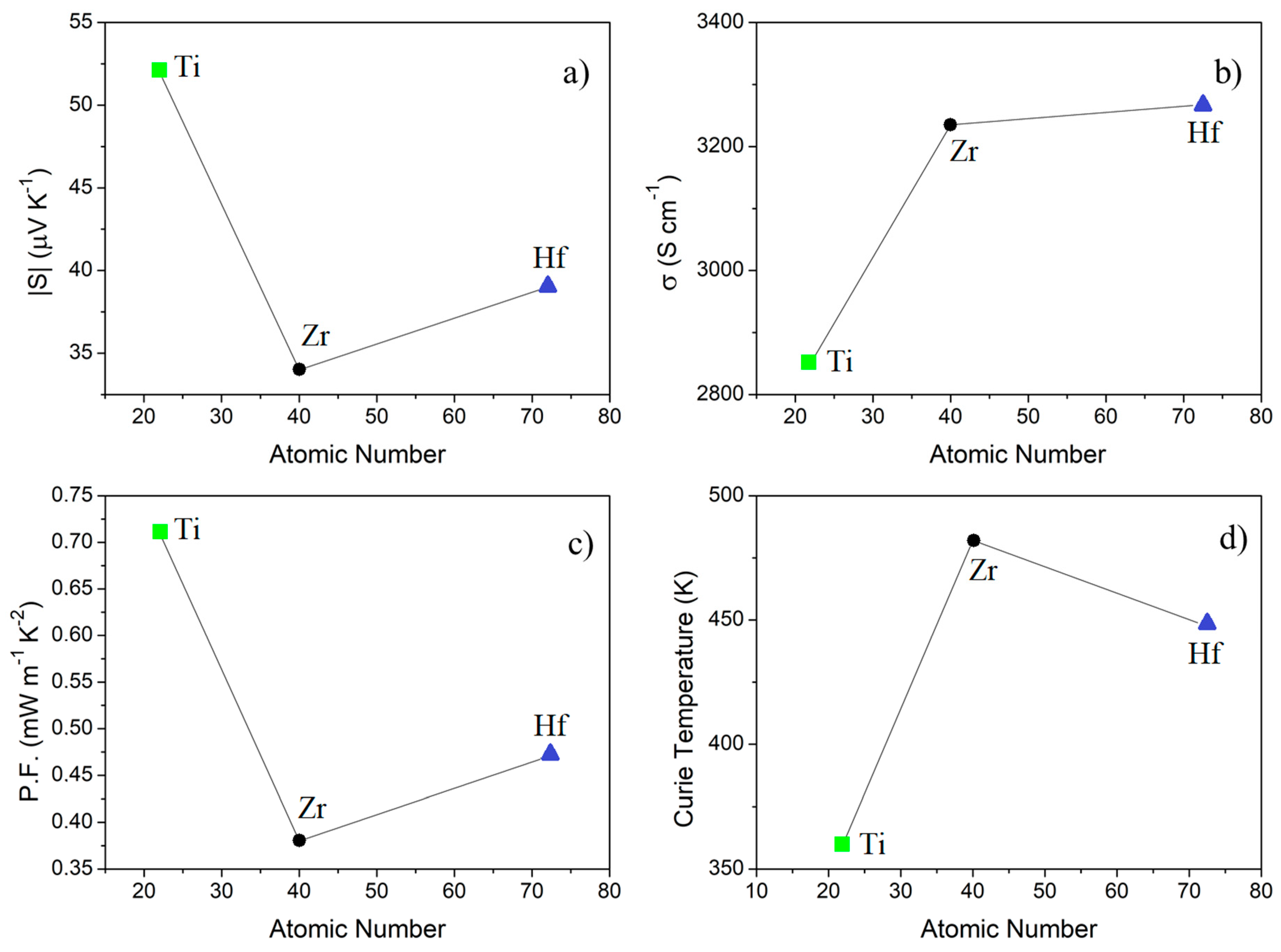
Metals Free Full Text Synthesis And Characterization Of Thermoelectric Co2xsn X Zr Hf Heusler Alloys

Los Annales Academiae Lugduno Batavae N S S B Pl Ij

Citroen Type H Food Truck 3d Model Max Obj Fbx Mat

Crease Export Fbx And Alembic Compatible With Other Softwares Blender Community

Can T Import Fbx Rig Into Ue4 Multiple Roots Found Maya Ue4 Answerhub

Ex 5 1 30 Find A And B Such That F X 5 Ax B 21

Blum Aventos Hf Modelo 3d 39 Max Obj 3ds Fbx Dwg Free3d

How To Convert Fbx To Obj 4 Easy Solutions All3dp

Solved Let 𝑓 𝑥 6 8𝑥 F X 6 8x Then The Expression 𝑓 𝑥 Chegg Com

El Desarrollo De La Chica Una Introduccion A La Embriologia Aves La Embriologia 134 El Desarrollo De Los Pichones Kfam S 16 Pr Atr Fig 71 Todo El Embrion De 16

Answered F 2 H F 2 If F X X Evaluate And Bartleby

3d Model Madrid Spain 80 Km Vr Ar Low Poly Obj 3ds Fbx C4d Stl

Elements Of Numerical Integration Ppt Download

Solved A Compute Maclaurin Series For The Following Func Chegg Com

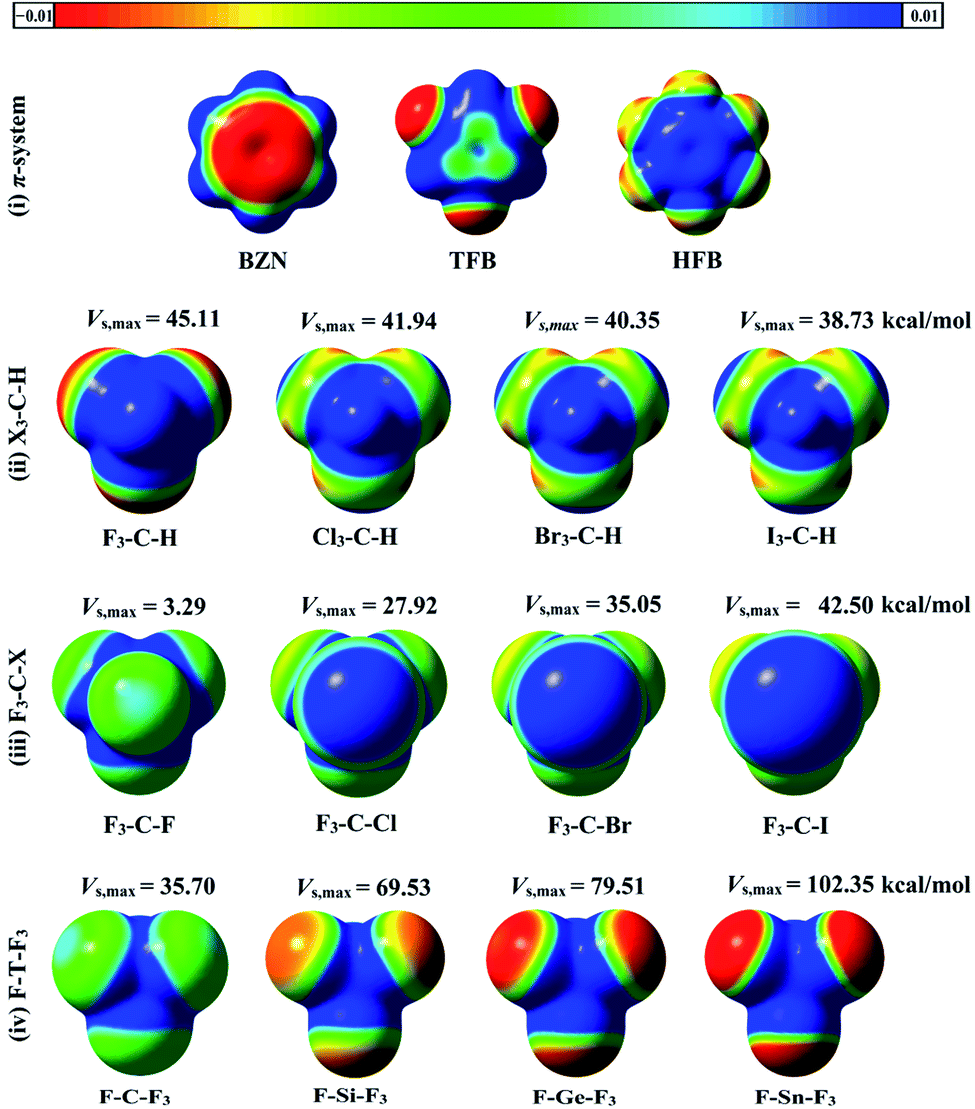
Comparative Investigation Of Interactions Of Hydrogen Halogen And Tetrel Bond Donors With Electron Rich And Electron Deficient P Systems Rsc Advances Rsc Publishing

Sea F X 1 X Halla A El Dominio De F B F 3 5 C F 3 D F 1 A E F X H F X H H Brainly Lat

X Ray Photoelectron Spectra Of Hf 4f Core Level For A Hfo X And B Download Scientific Diagram

Jumbo Lift 3500 Hf X Tend Unterflur Plataformas Elevadoras Para Talleres De Automoviles Made In Germany Desde Hace Mas De 40 Anos

Find A And B If F X Ax 2 B If F X X Sin X

Bombardero Xian H 6 Modelo 3d 149 X Wrl Obj Lwo Flt Fbx Dwg Dae Ma 3ds 3dm Max Unknown Free3d

Ti X Phase Diagrams Where X Is A Cr B Hf C Mo D Nb E Download Scientific Diagram

Explore 6 Haut Fourneau B Hfb Steelworks And Blast Furnace Belgium May 17 Adam X

Fbx File Format Cad Simply Explained All3dp

La Revista Filosofica De Londres Edimburgo Y Dublin Y La Revista Cientifica V 1 F L B E I R I1 T 4 J J

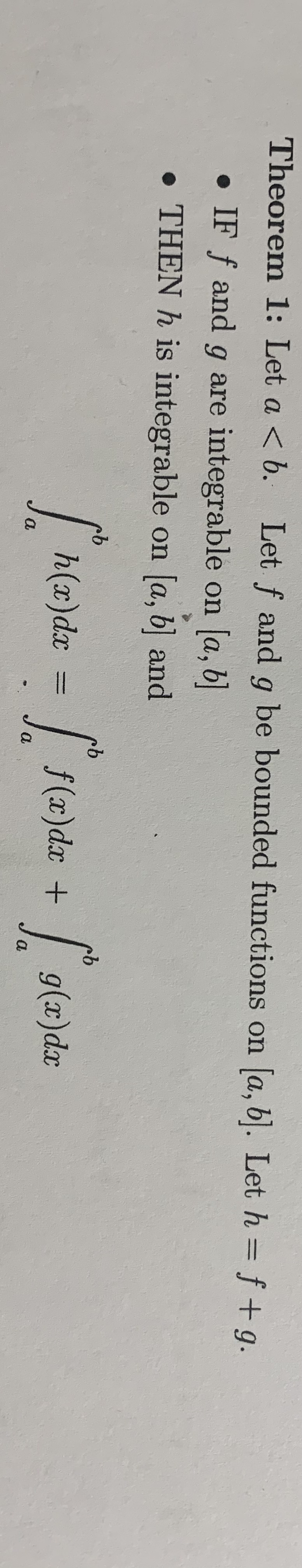
Answered Theorem 1 Let A B Let F And G Be Bartleby

Answered 5 X 5 Solve The Problem X B F 4 0 Bartleby

Inverse Trignometric Functions And Mean Value Theorem Mathematics Stack Exchange

Set Of Olive Trees Olea Europaea 3 Trees Modelo 3d In Arbol 3dexport

Sem Micrographies Of Samples A Polished Hf B Polished H 2 O 2 C Download Scientific Diagram

Truffle Hot Sauce Case Of 12 Hfb X Senor Lechuga Collaboration Sauc Half Face Blades

I Hoja 2 18 Examenes Studocu

Hannspree Hanns G Hs 275 Hfb 68 6 Cm 27 19 X 1080 Pixeles Full Hd Led Negro Gris 10 En El Stock De Distribuidores Mayoristas Para Que Lo Vendan Comercializadores Stock In The Channel

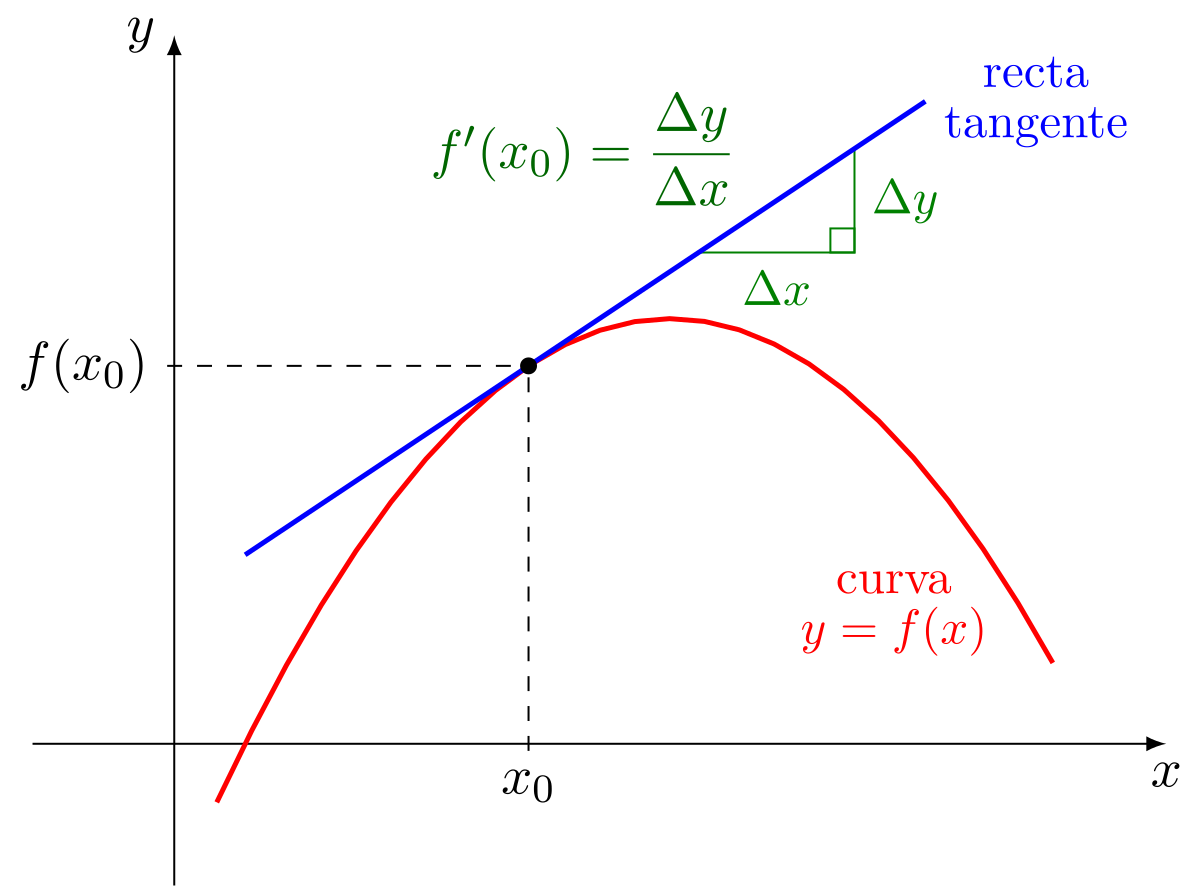
Derivada Wikipedia La Enciclopedia Libre

Solved Consider The Function 𝑓 𝑥 𝑥 4 F X X Chegg Com

Collectible Card Games Pokemon Supreme Victories Electivire Fb Lv X Holo 144 147 Nm Pokemon Trading Card Game

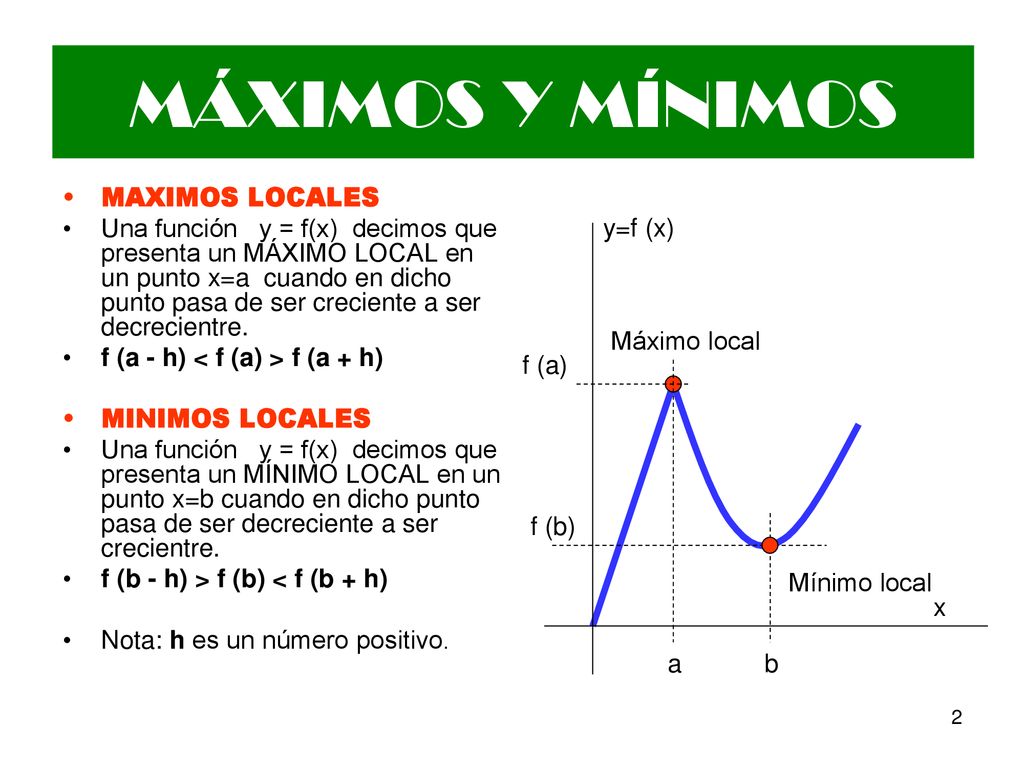
Mg Liz Robladillo Bravo Ppt Descargar

Practica 4 Audios Enunciado Practica 4 Studocu

Pin On 1080 Ham Rig 19

Cycling Sporting Goods 5mm X 35mm Wera 8740 B Hf Bit 3 8

Calculus Cheat Sheet All Flip Book Pages 1 11 Pubhtml5

Cars Making Car Lod S Simple Quick And Clean Racedepartment

Fresa Para Aluminio De 9 6 X 19 0 X 6 0 X 64 Mm Hf B Abrasivos Aplicados A La Soldadura Rhodius F

The Graph Of The F X Is Show Below Graph Each Transformed Function And List In Words The Transformation Used Socratic

Derivative Of Exponential Function What Does This Text Mean Mathematics Stack Exchange

Tinta Triangle Hpfb

Hf B 8 X 19 0 X 6 0 X 64 Fresa De Metal Duro Forma B Acero Inoxidable Rhodius

Funciones Medibles

Skeletal Animation Distorted Mesh For Fbx File But Not Dae File Stack Overflow

Skeletal Animation Distorted Mesh For Fbx File But Not Dae File Stack Overflow

If F X A Sinx B E X C X 3 And If F X Is Differentia

Megabass Dog X Giant Flotante Senuelo Hf Ito Tennessee Shad 9578 Ebay

Introductory Set Theory Pdf Free Download

Derivadas Y Sus Aplicaciones Apuntes De Teoria De La Argumentacion Juridica Docsity

Incoming Term: h x b x t, h u b f l i x,